20.2. RealWorldz Internals

Have you ever wanted to create your own personal planet? How would you go about this task? In this section, we go inside RealWorldz to examine the process of creating planets procedurally. We discuss the terrain-rendering structure, lighting and shadowing, fractal terrain generation, noise textures, tile set noise, surface normals, and height fields that allow for overhanging terrain. These concepts form the basis of the RealWorldz planetary rendering engine.

20.2.1. Terrain-Rendering Structure

RealWorldz uses a quadtree structure. Each node of the quadtree corresponds to a square patch of terrain and contains a vertex buffer object (VBO) and texture map for that patch. The four children of a node each cover one quarter of their parent's patch.

Rendering the planet is straightforwardthe tree is walked, with a level-of-detail (LOD) check made at each node. If a particular node would look polygonal when rendered, recursion continues to that node's children if possible. This LOD test determines which nodes should be subdivided to increase the terrain resolution in that area and which nodes are unnecessary and can be culled.

When a new node is created, the graphics accelerator generates the texture while the CPU generates the vertex data (in the future it is intended for the graphics hardware to generate the vertex data as well). To generate the texture for a new terrain node, the graphics hardware renders to the node's texture map using a specially constructed fragment shader. This fragment shader computes the fractal math needed to calculate the height and color of the terrain and carry out the lighting calculations, and it then outputs the final shaded color. The CPU and graphics hardware must carry out precisely the same calculations to compute the height and slope of each terrain pointif there's any difference, the terrain texture map will not follow the features of the terrain geometry. Imagine a planet with snow above a certain height. If the calculations to generate the texture map compute height in a different way from the calculations for the geometry, the snow line will obviously vary in height when the textured terrain is rendered.

20.2.2. Shading

No lighting is done when rendering terrainall lighting and shadowing is baked into the terrain texture map. This approach has several advantages: First, the fill rate for rendering terrain is improved because fewer calculations are done for each pixel, and only one texture map is read from (color) instead of two (color + normal). Second, this approach allows more complex lighting calculations since the lighting calculations are performed only once per texel, so they're not speed critical. Third, because the shading is completely separated from the geometry, the lighting does not change when the resolution of terrain geometry changes, that is, when terrain nodes are subdivided or collapsed. Therefore, the transition is less noticeable. Most significantly, this approach captures details at higher resolution than the geometry. (This idea is similar in spirit to normal maps.) However, the downside to the approach is that it cannot capture view-dependent lighting effects, such as specular highlights. But since terrain shading is diffuse rather than specular, this restriction is not an issue.

So, the fragment shader that generates the terrain texture maps calculates the color and surface normal for each texel, carries out the lighting calculations, and writes the resulting color to the texture map. When rendered, the color read from the texture map is affected only by atmospheric effects such as haze and fog.

20.2.3. Fractal Terrains

Fractal terrains are built by the combination of fractal functions, which themselves are built out of noise functions, such as those discussed in Chapter 15. The Perlin and Voronoi noise functions are particularly useful for creating fractal terrains. Perlin noise was described in Chapter 15. Voronoi noise (sometimes called cellular noise) is computed with the distance from points scattered randomly in space. This function produces a ridge along the line midway between two neighboring points.

A noise function is a function that is statistically invariant under translation and rotation and that has a reasonably narrow frequency range. A multifractal is computed by combining noise functions sampled at several different scales. The method of combining the noise function samples is what distinguishes one multifractal from another. For instance, the value of a monofractal with n octaves, with a given lacunarity L (a measure of how much the scale is changed for each successive noise function), offset, and roughness at the point x is defined as

Other multifractal types commonly used to define terrains are heterofractal and mountainfractal. They differ from monofractals in that the various noise samples are added or multiplied together in different ways.

The creation of interesting terrain is an artistic rather than mathematical process. Pandromeda's MojoWorld application is the most advanced tool for fractal planet generation available and produces compelling landscapes.

The landscapes in the images found on the MojoWorld gallery (http://www.pandromeda.com/gallery) are created by the combination of several multifractals, with the parameters of each multifractal carefully adjusted. The terrain shape is only a small part of the process: The terrain must also be colored, and the properties of the atmosphere, fog, clouds, water, stars, and sun edited to fit the artistic style of the terrain. The downside of having all this power available is that these images take hours to render.

MojoWorld includes a wide range of tools for constructing fractal planets, but only the ones that are the most useful and best suited tools for real-time use are implemented in RealWorldz. Such tools can combine multifractals by means of various mathematical operations (+, -, *, average) and can use one multifractal function to perturb the parameters fed into another.

In RealWorldz, the planet artist constructs a function tree to define the terrain. For instance, Figure 20.1 illustrates the function tree for the Ring world. This tree specifies a Voronoi mountainfractal distorted by the sine function, added to another distorted Voronoi multifractal, added to a Perlin heterofractal distorted by a monofractal.

Figure 20.1. Function tree for the Ring world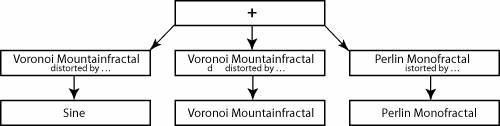

[View full size image]

The following node types are available for nodes in the RealWorldz function tree:

20.2.4. Fractal Terrains in RealWorldz

Fractal terrains rely on noise functions; it's not unusual for planets in MojoWorld to make use of a hundred octaves of noise. The speed of the noise function is therefore critical. It is straightforward to implement Perlin noise in the OpenGL Shading Language, but a naive implementation will require at least eight texture reads. Voronoi noise is substantially more complex than Perlin noiseand therefore slower. Even if artists were expected to limit themselves to 50 octaves of noise for a planet, and use only Perlin noise, over 400 texture lookups would be required for each evaluation of the terrain function, which would be impossibly slow.

The solution taken for RealWorldz is to use 2D instead of 3D noise, and instead of evaluating a 2D noise function, to use a texture map containing a periodic image of Perlin/Voronoi/Sine or like noise. These texture maps are called noise textures. Therefore, instead of the Perlin noise function being evaluated with parameters (x, y), a noise texture image is sampled at position (fract(x/k), fract(y/k)), where the noise texture is defined over the unit square. k is a factor to account for the scale of the noise textureit measures the size of the region to which the noise texture corresponds, whether the noise texture appears to be a 5 x 5 area of Perlin noise or a 50 x 50 area.

When implemented as a fragment shader, the fract operation is unnecessary if the texture wrap mode is set to GL_REPEAT.

It is easy to see the repeating pattern if a noise texture has only a handful of features, but with ten or more features along an axis, the repeating pattern is far more difficult to detect. On top of this, several noise textures of different periods will be combined in complex ways contributing to the shape of the terrain, obscuring the pattern even further.

20.2.5. Noise Texture Creation

The standard noise functions are Perlin, Voronoi, and Sine. Sine is periodic, so it is trivial to find a periodic 2D image of it. A ridged version of a noise function is created from the absolute value of the function to introduce ridges or is created from points at which the function folds back on itself (Perlin called this TURBULENCE).

In a nutshell, 2D Perlin noise is defined by interpolation between "hash values" given at integer coordinates. The value of Perlin noise at (3.6, 9.2) is found in this way: the hash function is evaluated at (3.0, 9.0), (4.0, 9.0), (3.0, 10.0) and (4.0, 10.0), and the four resulting values are combined. Creating Perlin-esque periodic noise of period k is done with the parameters to the hash function taken modulo k. All the different Perlin noise variantsgradient Perlin noise, value-gradient Perlin noise, ridged gradient Perlincan be handled this way.

The various Voronoi noise variants are built around a fixed pseudorandom scattering of key points on the plane. Basic Voronoi noise is defined as the distance to the closest key point. Other variants are the distance to the second closest key point, the third closest key point, the difference between the closest and second-closest key point, and so on. Making the distribution of the key points periodic with period k also makes the resulting Voronoi noise periodic.

20.2.6. Tile Set Noise

The noise texture pattern can be obscured even more with tiling. Instead of a single periodic image of noise, a set of noise tiles that have an identical boundary can be generated. A set of four such tiles is shown in Figure 20.2. These tiles can then be arranged randomly on the plane; the result might look like Figure 20.3. Each tile occupies the region on the plane from (u, v) to (u+1, v+1) for some integer u, v.

Sampling the noise function is now a two-stage process. Our goal is to find the appropriate noise value for the point (x, y). To accomplish this, we must first find the containing tile, then we must find the location to sample within that tile.

• The containing tile is located by first taking the integer part of x and y. Because tiles cover the region (u, v) to (u+1, v+1) for integer u, v, the values u and v are found by rounding x and y down to integers. These values are hashed and the result is taken modulo the number of tiles. The result is the noise tile to be accessed.

• Once the appropriate tile has been found, the address within the tile is p, q where p = x u, q = y v.

After these steps, we sample the appropriate tile and return the result. The implementation in a fragment shader is more efficient than this process might imply; it is described later.

The tile set can be generated with an extension of the method used to create periodic tiles. For the Perlin noise variants, the boundary hash points are fixed, whereas the interior hash points vary from tile to tile within the set. That is, for a region of period k, the hash point (0, 0) takes the same value for all tiles in the set; the hash point (1, 0) takes the same value for all tiles in the set, . . ., the hash point (k, 0) takes the same value for all tiles in the set. Similarly, the hash points (z, k), (0, z), and (k, z) take the same value for all tiles in the set, for any integer z in [0, k]. For the tiles to be periodic, the left and right edges of the tiles must match, as must the top and bottom edges. That is, the hashed values of the points (0, z) and (k, z) must be identical, as must the hashed values for the points (z, 0) and (z, k), for 0 z k.

Tile sets for the Voronoi noise variants can be generated similarly. The distribution of key points within a border region remains fixed for each tile in the set, while the distribution of key points in the rest of the tile varies from tile to tile. (This region in which the arrangement of key points changes from tile to tile is called the interior region.) The border region is found experimentally, by finding the smallest region such that the key points in the interior region of one tile have no effect on the noise function within a neighboring tile. For instance, if there are 33 key points within each tile, the border region is defined to be the region within 15% of the tile boundary. In other words: If the tile was unit sized, then the interior region is the points (x, y) for which x, y are in [0.15, 0.85), and the border region is the set of points (x, y) in the tile for which x or y is in [0, 0.15) [0.85, 1.0). For 100 points, the fixed border size is 10%.

20.2.7. Surface Normals

The easiest way to compute surface normals of fractal terrains is numerically. Find the neighbor points of the point in question, then use that information to estimate the shape of the surface and to establish a surface normal. In practice, the surface is often evaluated with a grid of points in parameter space, so surface normals can be found by taking the cross-product of the vectors between the four neighbors.

In a fragment shader, it is not possible to find the position of neighboring pointsthe environment is intentionally designed to allow fragment shaders for different fragments to execute in parallel. Also, the graphics card precision is 32-bit floating-point, and surface normals computed by subtraction of 32-bit floating-point positions have very noticeable banding patterns because work done in the range of magnitudes needed for large-scale terrain is imprecise.

The solution is to compute the surface normal analytically. In addition to storing a function value, noise textures also store the partial derivatives. The partial derivatives are then computed alongside the terrain height, and a surface normal is reconstructed as needed for lighting calculations.

For instance, a monofractal computed as described in Section 20.2.3 would have the 2D vector representing its partial derivative calculated as follows: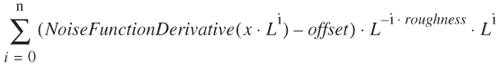

NoiseFunctionDerivative returns a 2D vector, where the x component is the partial derivative of the noise function with respect to x, and the y component is the partial derivative of the noise function with respect to y.

20.2.8. Overhanging Terrain

Some planets in RealWorldz have overhanging terrain, for instance, the AlienRockArt world as shown in Color Plate 36E. The method used to produce overhanging terrain addresses a more general problem: texture stretching on steep slopes of height field terrain. It is natural to texture-map a height field with a planar mapping; but on steep slopes the texture becomes very distorted.

Figure 20.4 demonstrates the problem. The cross marks on the graph are at evenly spaced parameter values. To put it another way, if this curve were a cross-section of some terrain that had been texture-mapped with planar mapping, then the crosses would correspond to evenly spaced points on the texture map. If the spacing between the crosses is reasonably constant, the texture map is stretched evenly across the terrain. If the spacing between the crosses varies, the texture is stretched unevenly.

In Figure 20.4, the distance between the crosses varies substantiallythe crosses on the steep parts are quite far apart compared to how close they are on the flat parts, which means that the texture will be quite distorted. The effect is that the steep parts of the terrain will seem to be quite blurry, while the flat parts of the terrain will have much a much sharper and cleaner appearance with more detail.

The goal is to produce steep terrain without texture distortion, that is, with a reasonably even spacing between crosses.

RealWorldz achieves the goal by postprocessing the height field terrain, making the terrain steeper. This step is called the "mushroom transformation." The two images in Figure 20.5 show the effect. The left image shows what could be the cross-section of a moderately steep hill. The right-hand image shows the vertices in the upper half of the hill pushed outward and the vertices in the bottom half pulled inward.

Figure 20.5. The "mushroom transformation" applied to a height field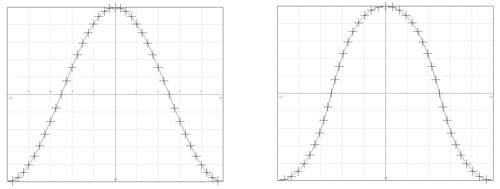

[View full size image]

More precisely, the transformation acts as follows. The terrain is defined as a height field: z = f(x, y). The terrain is made up of the set of points (x, y, f(x, y)).

The partial derivatives df/dx and df/dy are known, as are the maximum and minimum values of z: zmin and zmax. The point (x, y, f(x, y)) is offset by

where k is a constant specifying the degree of offset: 0 means no change. A larger value produced the right-hand image in Figure 20.5. Increasing the value still further gives a "mushroom look," so the constant k is called the "mushroom factor."

This equation is simpler than it appears. The partial derivative is converted into the vector (df/dx, df/dy, 0); the rest of the equation maps the z value from the range [zmin,zmax] to [0,2p] and takes the sine of that value. This sine value is responsible for pushing vertices out on the upper half (where the sine function is negative), and pulling vertices in on the lower half (where the sine function is positive). Vertices at the top, middle, and bottom (i.e., zmin, (zmin+zmax)*0.5, and zmax) are not moved. Figure 20.6 shows the effect of increasing values.

The distance between successive crosses is reasonably constant, so the texture mapping is good.

In practice, when this transformation is applied to a complex terrain, problems arise. If the terrain has high-frequency features, the derivatives vary considerably, and applying the mushroom transformation creates unrealistic horizontal spikes. The top of each hill won't achieve zmax, and the bottom of each valley won't reach zmin. For best results, the terrain should have a narrow frequency range.

The solution is to separate the terrain into two partstwo separate terrain function trees. The first component produces terrain without high frequencies and without large low-frequency features either, so the mushroom transformation can be applied. The second component is added to the first and does not have the mushroom transformation applied, so it can contain high- and low-frequency effects.

The Meran world (Color Plate 36C) is a good demonstration of how the two components are used. The shape of the stone lumps is defined by the first component, which has the mushroom transformation applied to give the bulblike shape. The second component of the terrain contributes everything else: the small ridges and wrinkles of the stone bulbs, and also the mountain ranges.

The mushroom effect is used on most of the worlds in a more subtle way, to produce steep slopes without texture distortion.