11.1. Regular Patterns

In Chapter 6, we examined a procedural shader for rendering bricks. Our first example in this chapter is another simple one. We try to construct a shader that renders stripes on an object. A variety of man-made objects can be rendered with such a shader: children's toys, wallpaper, wrapping paper, flags, fabrics, and so on.

The object in Figure 11.1 is a partial torus rendered with a stripe shader. The stripe shader and the application in which it is shown were both developed in 2002 by LightWork Design, a company that develops software to provide photorealistic views of objects created with commercial CAD/CAM packages. The application developed by LightWork Design contains a graphical user interface that allows the user to interactively modify the shader's parameters. The various shaders that are available are accessible on the upper-right portion of the user interface, and the modifiable parameters for the current shader are accessible in the lower-right portion of the user interface. In this case, you can see that the parameters for the stripe shader include the stripe color (blue), the background color (orange), the stripe scale (how many stripes there will be), and the stripe width (the ratio of stripe to background; in this case, it is 0.5 to make blue and orange stripes of equal width).

Figure 11.1. Closeup of a partial torus rendered with the stripe shader described in Section 11.1. (Courtesy of LightWork Design)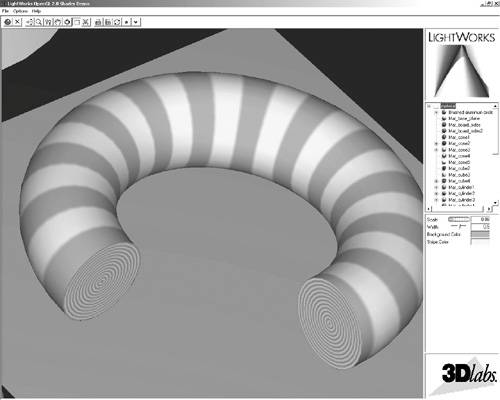

[View full size image]

For our stripe shader to work properly, the application needs to send down only the geometry (vertex values) and the texture coordinate at each vertex. The key to drawing the stripe color or the background color is the t texture coordinate at each fragment (the s texture coordinate is not used at all). The application must also supply values that the vertex shader uses to perform a lighting computation. And the aforementioned stripe color, background color, scale, and stripe width must be passed to the fragment shader so that our procedural stripe computation can be performed at each fragment.

11.1.1. Stripes Vertex Shader

The vertex shader for our stripe effect is shown in Listing 11.1.

Listing 11.1. Vertex shader for drawing stripes

uniform vec3 LightPosition; uniform vec3 LightColor; uniform vec3 EyePosition; uniform vec3 Specular; uniform vec3 Ambient; uniform float Kd; varying vec3 DiffuseColor; varying vec3 SpecularColor; void main() { vec3 ecPosition = vec3(gl_ModelViewMatrix * gl_Vertex); vec3 tnorm = normalize(gl_NormalMatrix * gl_Normal); vec3 lightVec = normalize(LightPosition - ecPosition); vec3 viewVec = normalize(EyePosition - ecPosition); vec3 hvec = normalize(viewVec + lightVec); float spec = clamp(dot(hvec, tnorm), 0.0, 1.0); spec = pow(spec, 16.0); DiffuseColor = LightColor * vec3(Kd * dot(lightVec, tnorm)); DiffuseColor = clamp(Ambient + DiffuseColor, 0.0, 1.0); SpecularColor = clamp((LightColor * Specular * spec), 0.0, 1.0); gl_TexCoord[0] = gl_MultiTexCoord0; gl_Position = ftransform(); }

There are some nice features to this particular shader. Nothing in it really makes it specific to drawing stripes. It provides a good example of how we might do the lighting calculation in a general way that would be compatible with a variety of fragment shaders.

As we mentioned, the values for doing the lighting computation (LightPosition, LightColor, EyePosition, Specular, Ambient, and Kd) are all passed in by the application as uniform variables. The purpose of this shader is to compute DiffuseColor and SpecularColor, two varying variables that will be interpolated across each primitive and made available to the fragment shader at each fragment location. These values are computed in the typical way. A small optimization is that Ambient is added to the value computed for the diffuse reflection so that we send one less value to the fragment shader as a varying variable. The incoming texture coordinate is passed down to the fragment shader as the built-in varying variable gl_TexCoord[0], and the vertex position is transformed in the usual way.

11.1.2. Stripes Fragment Shader

The fragment shader contains the algorithm for drawing procedural stripes. It is shown in Listing 11.2.

Listing 11.2. Fragment shader for drawing stripes

uniform vec3 StripeColor; uniform vec3 BackColor; uniform float Width; uniform float Fuzz; uniform float Scale; varying vec3 DiffuseColor; varying vec3 SpecularColor; void main() { float scaledT = fract(gl_TexCoord[0].t * Scale); float frac1 = clamp(scaledT / Fuzz, 0.0, 1.0); float frac2 = clamp((scaledT - Width) / Fuzz, 0.0, 1.0); frac1 = frac1 * (1.0 - frac2); frac1 = frac1 * frac1 * (3.0 - (2.0 * frac1)); vec3 finalColor = mix(BackColor, StripeColor, frac1); finalColor = finalColor * DiffuseColor + SpecularColor; gl_FragColor = vec4(finalColor, 1.0); }

The application provides one other uniform variable, called Fuzz. This value controls the smooth transitions (i.e., antialiasing) between stripe color and background color. With a Scale value of 10.0, a reasonable value for Fuzz is 0.1. It can be adjusted as the object changes size to prevent excessive blurriness at high magnification levels. It shouldn't really be set to a value higher than 0.5 (maximum blurriness of stripe edges).

The first step in this shader is to multiply the incoming t texture coordinate by the stripe scale factor and take the fractional part. This computation gives the position of the fragment within the stripe pattern. The larger the value of Scale, the more stripes we have as a result of this calculation. The resulting value for the local variable scaledT ranges from [0,1).

We'd like to have nicely antialiased transitions between the stripe colors. One way to do this would be to use smoothstep in the transition from StripeColor to BackColor, and use it again in the transition from BackColor to StripeColor. But this shader uses the fact that these transitions are symmetric to combine the two transitions into one.

So, to get our desired transition, we use scaledT to compute two other values, frac1 and frac2. These two values tell us where we are in relation to the two transitions between BackColor and StripeColor. For frac1, if scaledT/Fuzz is greater than 1, that indicates that this point is not in the transition zone, so we clamp the value to 1. If scaledT is less than Fuzz, scaledT/Fuzz specifies the fragment's relative distance into the transition zone for one side of the stripe. We compute a similar value for the other edge of the stripe by subtracting Width from scaledT, dividing by Fuzz, clamping the result, and storing it in frac2.

These values represent the amount of fuzz (blurriness) to be applied. At one edge of the stripe, frac2 is 0 and frac1 is the relative distance into the transition zone. At the other edge of the stripe, frac1 is 1 and frac2 is the relative distance into the transition zone. Our next line of code (frac1 = frac1 * (1.0 - frac2)) produces a value that can be used to do a proper linear blend between BackColor and StripeColor. But we'd actually like to perform a transition that is smoother than a linear blend. The next line of code performs a Hermite interpolation in the same way as the smoothstep function. The final value for frac1 performs the blend between BackColor and StripeColor.

The result of this effort is a smoothly "fuzzed" boundary in the transition region between the stripe colors. Without this fuzzing effect, we would have abrupt transitions between the stripe colors that would flash and pop as the object is moved on the screen. The fuzzing of the transition region eliminates those artifacts. A closeup view of the fuzzed boundary is shown in Figure 11.2. (More information about antialiasing procedural shaders can be found in Chapter 17.)

Figure 11.2. Extreme closeup view of one of the stripes that shows the effect of the "fuzz" calculation from the stripe shader. (Courtesy of LightWork Design)

[View full size image]

Now all that remains to be done is to apply the diffuse and specular lighting effects computed by the vertex shader and supply an alpha value of 1.0 to produce our final fragment color. By modifying the five basic parameters of our fragment shader, we can create a fairly interesting number of variations of our stripe pattern, using the exact same shader.