10.6. Glyph Bombing

In this section, we develop a shader that demonstrates a couple of different uses for textures. In Texturing and Modeling: A Procedural Approach, Darwyn Peachy described a process called TEXTURE BOMBING that creates an irregular texture pattern. The idea is to divide a surface into a grid, and then draw a decorative element or image (e.g., a star, a polka dot, or some other shape) within each cell. By applying some randomness to the placement, scaling, or rotation of each texture element, you can easily create an interesting pattern that is suitable for objects such as wallpaper, gift wrap, clothing, and the like. Peachey described a RenderMan shader to perform texture bombing, and in GPU Gems, Steve Glanville described a method for texture bombing in Cg.

The basic concept of texture bombing can be taken a bit further. Joshua Doss developed a GLSL shader that randomly selects from several collections of related character glyphs. Two textures are used for the so-called GLYPH BOMBING shadera single texture that stores character glyphs and a texture that stores random values. Let's examine how this shader works.

10.6.1. Application Setup

The first step is to create a 2D texture that contains the glyphs that will be used. To set this up, you just need to carefully draw characters on a 10 x 10 grid, using a 2D image editing program like Photoshop. Each row should have a common theme like the image shown in Figure 10.3. A single uniform variable (ColAdjust) is used to select the row to be accessed. Within this row, a glyph is chosen at random, and when it is drawn, it can also be optionally scaled and rotated. Thus, we can easily choose a pattern from a collection snowflakes, musical symbols, animal silhouettes, flower dingbats, and so on. Applying a random color and placing the glyph randomly within the cell add even more irregularity and interest to the final result.

The second texture that this shader uses contains random values in the range of [0,1.0] for each component. We access this texture to obtain a vec4 containing random numbers and use these values to apply randomness to several computations within the fragment shader.

Just like the brick shader discussed in Chapter 6, this shader needs a frame of reference for creating the cells in which we draw our glyphs. In this case, we use the object's texture coordinates to establish the reference frame. We can scale the texture coordinates with a uniform variable (ScaleFactor) to make the cells larger or smaller. Our glyph texture map contains only levels of gray. We use the value obtained from the glyph texture map to linearly interpolate between a default object color (ModelColor) and a random color that is generated when a glyph is drawn.

Because we are allowing random offsets and random rotation, we need to take care of some complications in our shader. Each of these effects can cause the object we are drawing to extend into neighboring cells.

Let's first consider the case of random offsets. When each glyph is drawn, our shader offsets the glyph by adding a value in the range [0,1.0] for each of x and y. This means that the glyph can be shifted over and up by some amount, possibly contributing to the contents of pixel locations in three neighboring cells to the right and above. Figure 10.4 illustrates the possibilities.

Consequently, as we consider how to compute the value at one particular pixel location, we must consider the possibility that the glyphs to be drawn in cells to the left and below the current cell may be contributing to the fragment. For instance, the spot marked by the x in Figure 10.4 might actually have contributions from the glyphs in cells (m, n), (m+1, n), and (m, n+1) in addition to the glyph contained in the cell (m+1, n+1).

Things get even more interesting when we allow for a random angle of rotation. Now the offset combined with rotation can cause our glyph to extend into any of nine cells, as shown in Figure 10.5. For this case, as we render fragments we must consider all eight surrounding cells in addition to the cell containing the fragment being rendered. We use a Boolean uniform variable, RandomRotate, to determine whether we need to loop over four cells or nine.

Figure 10.5. Depending on a random offset and a random angle of rotation, a glyph may contribute to fragments in any of nine adjacent cells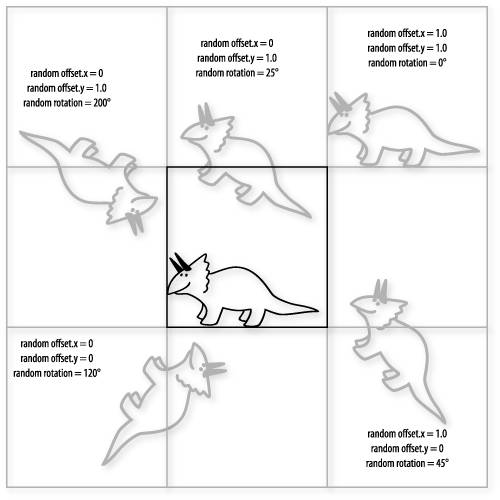

[View full size image]

We use a few additional uniform variables to offer more control over the number of glyphs and their placement and to give an even greater appearance of randomness to the final pattern. RandomScale is a Boolean value that causes the size of the glyph to be scaled in both x and y by random values in the range [0,1.0]. (This has no effect on the cells that are affected, because the glyph can only be made smaller by this operation.) Another uniform variable, Percentage, indicates the probability that a glyph will be drawn in each cell. Lowering this value increases the number of empty cells in the final image.

We can even include a loop in the shader so that we can apply more than one glyph per cell. The number of glyphs drawn per cell is set with SamplesPerCell. Setting this value to increasingly higher values will bring any graphics hardware to its knees. If random rotation is enabled, the fragment shader will need to iterate over nine cells and within each of these cells loop SamplesPerCell times in order to draw all the glyphs. This is a lot of computation at every fragment!

The uniform variables for this shader and their initial values are

SpecularContribution	0.2
LightPosition	4.0, 14.0, 4.0
ScaleFactor	10.0
ModelColor	1.0, 1.0, 1.0, 1.0
GlyphTex	0
RandomTex	1
ColAdjust	0.75
Percentage	1.0
SamplesPerCell	1.0
R01	0.29
RandomScale	false
RandomRotate	false

10.6.2. Vertex Shader

Listing 10.9 contains the vertex shader for glyph bombing. The only differences between this shader and the vertex shader for bricks discussed in Chapter 6 are that the diffuse factor is multiplied by a somewhat arbitrary factor of two and that the scaled texture coordinates are passed to the fragment shader to form the frame of reference for defining the cells into which glyphs will be drawn.

Listing 10.9. Vertex shader for doing glyph bombing

uniform float SpecularContribution; uniform vec3 LightPosition; uniform float ScaleFactor; varying float LightIntensity; varying vec2 TexCoord; void main() { vec3 ecPosition = vec3(gl_ModelViewMatrix * gl_Vertex); vec3 tnorm = normalize(gl_NormalMatrix * gl_Normal); vec3 lightVec = normalize(LightPosition - ecPosition); vec3 reflectVec = reflect(-lightVec, tnorm); vec3 viewVec = normalize(-ecPosition); float diffuse = max(dot(lightVec, tnorm), 0.0); float spec = 0.0; if(diffuse > 0.0) { spec = max(dot(reflectVec, viewVec), 0.0); spec = pow(spec, 16.0); } float diffusecontribution = 1.0 - SpecularContribution; LightIntensity = diffusecontribution * diffuse * 2.0 + SpecularContribution * spec; TexCoord = gl_MultiTexCoord0.st * ScaleFactor; gl_Position = ftransform(); }

10.6.3. Fragment Shader

Listing 10.10 contains the fragment shader for glyph bombing. As you can see, this shader makes heavy use of looping. The first step is to assign the base color for the fragment, and then compute the fragment's cell and position within the cell. As we iterate through the loops, the value for color accumulates the color for the current fragment, which may be covered by multiple glyphs of different colors. A double for-next loop lets us iterate across four cells if RandomRotate is false (0) and across nine cells if it is true (1). This double loop determines whether any of the neighboring cells contain a glyph that contributes to the fragment currently being computed.

For each iteration of the inner loop, we need to determine whether the glyph in the neighboring cell affects the fragment that is being rendered. This requires that we compute the cell number for each neighboring cell as well the offset from the lower-left corner of the neighboring cell to the current fragment.

We use the cell value to compute the initial index value used to access our random number texture. This provides the beginning of a repeatable sequence of random numbers used for the calculations within that cell. This means that whenever we consider the contents of this cell, we always compute the same random glyph, the same random offset, and so on.

To start the random number sequence in a different location for each of the cells, during each loop iteration we compute the index into our random texture by multiplying the current cell value by a uniform variable (RO1) that a user can adjust to achieve pleasing results.

At this point, we enter yet another loop. This loop iterates over the number of samples per cell. Within this loop, the first thing we do is access our random number texture to obtain four random numbers in the range [0,1.0]. The result of this operation is a variable (random) that we use in performing a number of computations that require an element of randomness. To avoid using the same random number for each iteration of this loop, we add the third and fourth components of the random number to our random texture index. We use this value to access the texture in the next iteration of the loop. Now we get to the heart of the glyph bombing algorithm.

If the first component of the random number we've obtained is greater than or equal to Percentage, we exit the loop, use the color value computed thus far as the value for the fragment, and are done with the computation concerning this particular cell. Otherwise, we must generate a value that can index into our glyph texture. The first steps are to use ColAdjust to select the row of our glyph texture (index.t) and then select a random glyph within that row (index.s). Multiplying by 10 and using the floor function divides the texture into 10 sections in each direction. This gives us access to the 100 separate glyphs.

The next thing we need to do is compute a value that can access the proper texel in the glyph for this particular cell (glyphIndex). Here the offset, rotation, and scaling factors come into play. If RandomRotate is true, we generate a random angle of rotation, compute the corresponding rotation matrix, and use this matrix to transform the texture coordinates for accessing the glyph. This value is then combined with the random offset for the glyph. If we're not doing rotation, we just apply the random offset.

(Interestingly, the fragment shader for drawing glyphs never actually has to add the random offsets for drawing glyphs. Instead, the fragment shader assumes that the random offsets have been added and computes whether a glyph in a neighboring cell contributes to the current fragment by subtracting the random offset and then doing a texture lookup for the glyph in the neighboring cell. This is an example of the type of logic that is sometimes needed to convert a rendering algorithm into a fragment shader.)

The next step is to apply random scaling to the texture coordinates. random.r is a value in the range [0, 1.0]. If we divide our glyph index by this value, the glyph index values (i.e., the coordinates used to access the glyph) get larger. And if the coordinates used to access the glyph get larger, the apparent size of the glyph that is drawn gets smaller. By multiplying random.r by 0.5 and adding 0.5, we constrain the random scaling to be between 50% and 100% of the original size.

The resulting texture coordinates are clamped to the range [0,1.0], added to the index of the glyph that is rendered, divided by 10, and then used to access the glyph texture. All the glyphs in our glyph texture have at least one pixel of white along each edge. By clamping the values to the range [0,1.0] we effectively say "no contribution for this glyph" whenever the glyph index values exceed the range [0,1.0]. If the glyph value obtained is a color other than white, we use the resulting texture value to linearly interpolate between the color value computed thus far and a random color. Because the glyph texture contains only levels of gray, the comparison is only true for texels other than pure white. The mix function gives us a smoothly antialiased edge when the glyph is drawn, and it allows us to properly layer multiple glyphs of different colors, one on top of the other.

Listing 10.10. Fragment shader for doing glyph bombing

#define TWO_PI 6.28318 uniform vec4 ModelColor; uniform sampler2D GlyphTex; uniform sampler2D RandomTex; uniform float ColAdjust; uniform float ScaleFactor; uniform float Percentage; uniform float SamplesPerCell; uniform float RO1; uniform bool RandomScale; uniform bool RandomRotate; varying vec2 TexCoord; varying float LightIntensity; void main() { vec4 color = ModelColor; vec2 cell = floor(TexCoord); vec2 offset = TexCoord - cell; for (int i = -1; i <= int (RandomRotate); i++) { for (int j = -1; j <= int (RandomRotate); j++) { vec2 currentCell = cell + vec2(float(i), float(j)); vec2 currentOffset = offset - vec2(float(i), float(j)); vec2 randomUV = currentCell * vec2(RO1); for (int k = 0; k < int (SamplesPerCell); k++) { vec4 random = texture2D(RandomTex, randomUV); randomUV += random.ba; if (random.r < Percentage) { vec2 glyphIndex; mat2 rotator; vec2 index; float rotationAngle, cosRot, sinRot; index.s = floor(random.b * 10.0); index.t = floor(ColAdjust * 10.0); if (RandomRotate) { rotationAngle = TWO_PI * random.g; cosRot = cos(rotationAngle); sinRot = sin(rotationAngle); rotator[0] = vec2(cosRot, sinRot); rotator[1] = vec2(-sinRot, cosRot); glyphIndex = -rotator * (currentOffset - random.rg); } else { glyphIndex = currentOffset - random.rg; } if (RandomScale) glyphIndex /= vec2(0.5 * random.r + 0.5); glyphIndex = (clamp(glyphIndex, 0.0, 1.0) + index) * 0.1; vec4 image = texture2D(GlyphTex, glyphIndex); if (image.r != 1.0) color.rgb = mix(random.rgb * 0.7, color.rgb, image.r); } } } } gl_FragColor = color * LightIntensity; }

This particular shader was designed for flexibility in operation, not performance. Consequently, there are enormous opportunities for making it run faster. There are two texture accesses per iteration of the innermost loop, so enabling rotation and having five samples per cell implies 90 texture accesses per fragment. Still, there are times when some of the techniques demonstrated by this shader come in handy. Some images that demonstrate the flexibility of this shader are shown in Figure 10.6, Figure 10.7, and Color Plate 8.